『사경인의 친절한 투자과외』 중에서
투자의 가성비
A : +20%, -10%, 평균 +5%
B : +30%, -20%, 평균 +5%
C : +40%, -30%, 평균 +5%
A, B, C의 투자 수익률의 산술평균 모두 +5%로 같다. 실제로는 어떨까?
10,000원을 투자했을 경우
A : 10,000원 → 12,000원(+20%) → 10,800원(-10%), 결과 +8%
B : 10,000원 → 13,000원(+30%) → 10,400원(-20%), 결과 +4%
C : 10,000원 → 14,000원(+40%) → 9,800원(-30%), 결과 –2%
똑같이 평균은 5%로 인데 결과는 다 다르게 나온다. 이렇듯 변동성이 얼마냐에 따라 결과가 달라진다. 변동성이 크면 위험하다, 수익률이 나빠질 수 있다.
이는 산술평균과 기하평균의 차이이기도 하다. 산술평균(더하기 평균)은 이겼을 때와 졌을 때의 결과를 더해서 둘로 나누니 평균이 5%로 같지만, 기하평균(곱하기 평균)은 이겼을 때와 졌을 대의 결과를 곱해서 루트를 씌워 나누기 때문에 결과가 모두 달라지게 된다.
결국, 똑같이 평균이 5%라도 변동성이 크면 결국에 수익률이 나빠질 수 있다.
마음고생을 나타내는 지표 M.D.D
MDD란, Maximum Draw Down의 약자로 최대 낙폭을 의미한다. 제일 꼭대기에서 제일 바닥까지가 얼마나 되는지를 수치화한 것으로 MDD가 클수록 마음고생이 크다. 따라서 수익률이 같더라도 MDD가 크면 별로 안 좋은 투자가 될 수 있다.
아파트의 경우 5억에 사서 5억에 팔았다고 하더라도, 그 10년 동안 내가 거주한 거주비용이 절약되거나, 세를 놓아 월세를 한 달에 30만 원씩 받을 수도 있다. 즉, 들고 있는 동안 내가 받는 돈도 수익률 계산에 넣어야 하는데 이를 보유수익이라고 하고, 주식의 경우는 배당금이 이에 해당된다. 이 보유수익률을 합산한 것이 합계수익률이다.
과거 20년간 코스피지수와 아파크가격지수의 MDD비교
| 코스피지수 | 아파트가격지수 | |||
| 평균값 | 중간값 | 평균값 | 중간값 | |
| 수익률(CAGR) | 7.89% | 5.73% | 4.44% | 3.43% |
| MDD | 40.78% | 47.60% | 1.91% | 1.88% |
| 보유수익률 | 1.44% | 1.35% | 3.73% | 3.69% |
| 합계수익률 | 9.33% | 7.08% | 8.17% | 7.12% |
주식과 아파트의 합계수익률이 거의 비슷한데, 주식은 마음고생이 훨씬 심하다는 것을 알 수 있다. 언론에서 단순히 지수수익률 중간값만 비교해서 주식이 더 좋고, 장기 보유하면 주식수익률이 더 높다고 얘기하는데, 보유수익을 더한 합계수익률은 큰 차이가 없을 뿐 더러, MDD도 크다.
주식과 부동산 투자의 장단점
| 주식 | 부동산 | |
| 장점 | · 장기보유 시 높은 기대수익 · 소액으로 투자 가능 · 낮은 세부담과 수수료 유지비용 · 매매가 자유로움 |
· 상대적으로 높은 보유이익 · 낮은 변동성 · 적극적 수익성 개선 가능(리모델링 등) |
| 단점 | · 높은 변동성으로 인한 고통 · 매매가 자유로움 |
· 종잣돈이 있어야 투자 가능 · 매매가 자유롭지 못함 · 상대적으로 높은 세금부담 |
주식이 부동산에 비해 가진 장점은 아래 두 가지 정도다.
① 세금 (보유, 거래수수료, 양도세 등)
② 소액 투자 가능
단, 부동산의 경우 전체 평균 수치로 주식과 수익률을 비교할 수 있지만, 주식시장의 인덱스펀드처럼 전체를 다 살 수는 없다. 특정 아파트를 찍어서 사야하기 때문에 개인의 선택에 따른 수익률 편차가 심할 수 있다.
나눠서 투자하면 좋은 이유
주식과 부동산이 모두 장단점이 있다면, 주식과 부동산에 분산 투자하는 것은 어떨까?
투자금 20,000원이 있다. A랑 B를 10,000원씩 나누어 산다고 했을 때, A는 10%씩 오르고, B는 10%씩 떨어졌다고 가정해보자. 결과는 어떠할까?
A : 10,000원 → 11,000원(+10%) → 12,100원(+10%), 결과 +21%
B : 10,000원 → 9,000원(-10%) → 8,100원(-10%), 결과 -19%
A+B : 20,000원 → 20,200원, 결과 +2%
하나는 10%씩 오르고, 하나는 10%씩 떨어졌는데 본전이 되는 게 아니라, 2%의 수익률이 나왔다.
투자금 20,000원을 시간을 나누어 투자하면 어떻게 될까? 투자 기간을 반으로 쪼개어 한 달은 A(+10%)에 전액투자하고, 다음 달은 B(-10%)에 투자한다고 해보자.
A+B : 20,000원 → 22,000원(+10%) → 19,800원(-10%), 결과 -1%
B+A : 20,000원 → 18,000원(-10%) → 19,800원(+10%), 결과 -1%
똑같이 10%씩 오르고 내렸지만 결과는 모두 –1%가 나왔다.
결국, 두 자산에 돈을 나눠서 투자하면 이익이 났고, 시간을 나눠서 투자하면 손해가 났다.
대상을 나눠서 투자하는 걸 분산투자라고 하고, 시간을 나누면 단기투자라고 한다. 우리가 추구해야 할 것은 분산투자이자, 장기투자임을 알 수 있다.
분산투자한 사람들이 집중투자한 사람들에 비해서 평균적으로는 더 결과가 좋다. 그런데 가장 좋은 결과를 내는 건 집중투자한 다음에 연속해서 적중한 사람들이다. 사람들은 크게 돈을 번 부자들에게만 관심을 가지는데 큰 돈을 번 사람들에게 어떻게 부자가 됐냐고 물어봤더니 대부분 집중투자했다고 말했다. 그래서 집중투자를 해야 부자가 되는구나 생각한다. 1,000명이 모여서 가위바위보를 하면 10번 연속 이기는 사람은 꼭 나오게 되어 있다. 투자자들 중에도 10번 연속 찍어서 맞추는 사람이 나올 수밖에 없다. 실제로는 그보다 훨씬 많은 사람들이 집중투자 때문에 망했는데, 망한 사람들은 눈에 보이지 않는 것이다.
결국, 분산투자, 장기 투자해야 한다. 이것이 천천히 부자가 되는 길이다.
손실게임을 수익게임으로 바꾸는 도박사의 공식
위에서 10,000원을 투자하여 한번은 40%로 오르고 한 번은 30% 떨어질 경우 결과는 다음과 같았다.
C : 10,000원 → 14,000원(+40%) → 9,800원(-30%), 결과 –2%
만약 내가 가진 돈을 전부 투자하지 않고, 항상 가진 돈의 절반만 투자하는 경우 어떻게 될까?
C1 : 5,000원 → 7,000원(+40%)
5,000원 → 5,000원(현금), 결과 12,000원(+20%)
C2 : 6,000원 → 4,200원(-30%)
6,000원 → 6,000원(현금), 결과 10,200원(-15%)
C1+C2 : 10,000원 → 10,200원, 결과 +2%
똑같은 게임을 했는데 절반씩 투자할 경우 변동성이 줄어들어 이익이 나게 되었다. 도박사들은 이렇게 내가 가진 돈의 몇 %씩을 투자해야 제일 좋은 결과가 나오느지를 계산하여(켈리 방정식) 배팅을 한다. 투자에서는 이를 자금관리나 포트폴리오라고 부른다. 포트폴리오란 내 자산을 어디에 얼마씩 배분할 것인지를 정하는 것이다.
따라서 투자하기 전에 주식에 얼마를 투자할지, 내가 가진 자산 중에 몇 %를 투자할지를 정해야 한다. 고수에게 아무리 좋은 종목을 좋은 타이밍이나 가격에 추천받아 사고 팔더라도 자산배분 비율을 정하지 않고 시작하면, 배팅이 잘못되어 똑같은 돈을 투자했는데 고수는 돈을 벌지만 초보자는 돈을 잃는 결과가 나올 수 있는 것이다. 자산을 배분하는 방법이나, 투자의 원리를 모르는 상태에서는 십중팔구 돈을 잃을 수 밖에 없다.
사경인의 투자 숙제
직접 MDD를 계산해보자.
투자 경험이 있거나 관심 있는 종목의 10년 주가 그래프를 대략 그려보기
그래프의 주가를 표시한 후 10년 기간 동안의 MDD를 대략 계산해보기
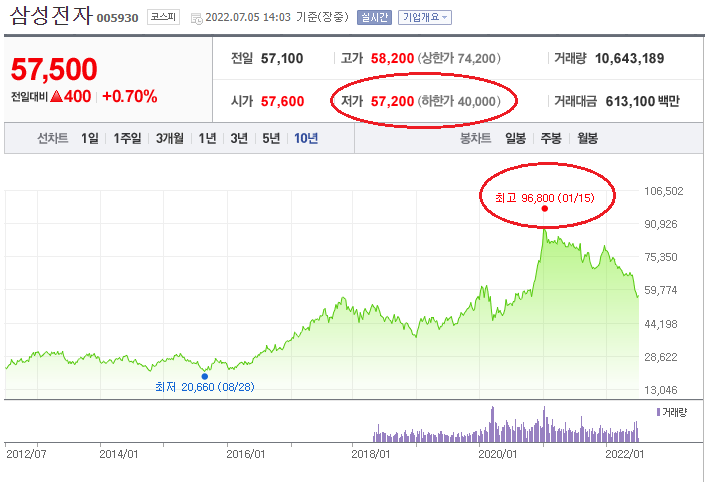
삼성전자의 전고점은 96,800원이다. 이후 하락하기 시작하여 현재 2022년 7월 57,200원이 저점이라고 가정할 때, 전고점 대비 39,600원까지 하락했다. MDD 40.9%다.
'☆ 경제·투자·재테크 > 주식 관련' 카테고리의 다른 글
| 포트폴리오 비쥬얼라이저(백테스트 하는 법) (0) | 2022.07.07 |
|---|---|
| 자산배분, 어떻게 할 것인가?(코스톨라니의 달걀) (0) | 2022.07.06 |
| 강남 아파트 vs 삼성전자 어디에 투자하는 것이 더 유망할까? (0) | 2022.07.04 |
| 투자를 망치는 사람들의 심리 편향 (0) | 2022.05.27 |
| [주식용어] 보통주와 우선주 개념(feat. 배당) (0) | 2021.11.11 |


